コンピュータ上で扱われる数値と表記法
現在使われているコンピュータの内部では、基本的に0と1の二種類の数値しか扱えません。
昔は、回路に電気が通っているか(On=1)通っていないか(Off=0)情報を数値に置き換えて処理していましたが、現在は回路に流れている電圧が高いか(On=1)低いか(Off=0)で区別しているそうです。
大きい数値を扱いたい場合は、On Offの組み合わせを1桁として、複数桁を処理する事にしました。
この方法が一番計算回路がシンプルになって計算ミスが出にくいという事を、元マサチューセッツ工科大学教授のクロード・エルウッド・シャノン(Claude Elwood Shannon 1916-2001)が証明しました。シャノンの情報理論は、現在のコンピュータを初めとする通信回路設計のための基礎的な理論となっています。
0と1の二種類で数値を表記する方法は2進法と呼ばれ、ドイツのライプニッツが17世紀に体系化しました(通常用いる10進数との比較は下表を参照してください)。2進法で表記された数値は「2進数(binary number)」と呼びます
| 10進法 | 2進法 | 16進法 |
|---|---|---|
| 0 | 0 | 0 |
| 1 | 1 | 1 |
| 2 | 10 | 2 |
| 3 | 11 | 3 |
| 4 | 100 | 4 |
| 5 | 101 | 5 |
| 6 | 110 | 6 |
| 7 | 111 | 7 |
| 8 | 1000 | 8 |
| 9 | 1001 | 9 |
| 10 | 1010 | A |
| 11 | 1011 | B |
| 12 | 1100 | C |
| 13 | 1101 | D |
| 14 | 1110 | E |
| 15 | 1111 | F |
| 16 | 10000 | 10 |
但し、2進法では数値の桁数が増えると、視覚的に判読しづらくなります。
また、2進数と私たちが日常使用する10進数の相互変換も計算式が必要となり面倒です。
10進法の10000→2進法では10011100010000
そのため、通常コンピュータ上のデータ配列は、2進法ではなく16進法で表記します。
それぞれの換算方法は、下の記述を参照してください。
10進法から2進法への換算方法
例:10進法表記(10進数)の[35]を2進法表記(2進数)に換算する
10進法の数値を先頭の桁から順に2で割ります。
35÷2=17(商) 余り 1
余りを2進数下一桁の数値とします
1
前の計算の商をまた2で割ります
17÷2=8 余り 1
余りを2進数の次桁の数値にします
11
(以下繰り返し)
8÷2=4 余り 0 → 011
4÷2=2 余り 0 → 0011
2÷2=1 余り 0 → 00011
1÷2=0 余り 1 → 100011
結果、[100011]となります。
2進数から10進数への換算方法
例:[101000]を10進数に換算
2進数から10進数に変換するには、それぞれの桁の数値を2の(各桁数-1)乗して、最後にそれを合計します。
下一桁目
0の2の(1-1)乗=0×2^0=0×1=0
下二桁目
0の2の(2-1)乗=0×2^1=0×2=0
下三桁目
0の2の(3-1)乗=0×2^2=0×4=0
下四桁目
1の2の(4-1)乗=1×2^3=1×8=8
下五桁目
0の2の(5-1)乗=0×2^4=0×16=0
下六桁目
1の2の(6-1)乗=1×2^5=1×32=32
各桁の計算結果を合計
0+0+0+8+0+32=40
結果、[40]となります。
ちなみに、2の乗数は以下の通りです。
| 2の乗数 | 数値 |
|---|---|
| 0 | 1 |
| 1 | 2 |
| 2 | 4 |
| 3 | 8 |
| 4 | 16 |
| 5 | 32 |
| 6 | 64 |
| 7 | 128 |
| 8 | 256 |
| 9 | 512 |
| 10 | 1024 |
16進法について
「16進法」とは、一桁を0~9,A~Fの16種類の数値で表記する表記法です。
16進法で表記された数値は「16進数(hexadecimal number)」と呼びます。また、ある数値が16進数であることを明示するために、数値の頭に「0x」「&H」をつけたり、16進数を「0」「H」で挟んで表記する場合場あります。
16進法で表記すると、大きい桁になればなるほど、2進法に比べてデータ表記が短くて済むというメリットがあります。
また、16進法は2進法からの数値換算が10進法に比べて非常に簡単であるというメリットもあり(換算方法は次の項目を参照してください)、コンピュータ上で扱われる数値を表記する際には、一般に16進法が採用されています。
2進数と16進数との換算方法
ここでは2進数10011100010000(10進数10000)の換算について説明します。
2進数から16進数への換算
初めに、2進数を下から4桁ずつに区切ります。
10011100010000 を (00)10 0111 0001 0000 のように切り分けます。
次に、4桁ごとで切り分けた2進数の数値を、上の表を見て16進法表記に換算します。
0010→2 0111→7 0001→1 0000→0 (但し、桁揃えの0は省略)
換算結果:2710
16進数から2進数への換算
16進数を2進数に変換する場合は、この手順を逆に行ってください。
初めに、「2710」を 「2」 「7」 「1」 「0」 の四つに切り分けます。
次に、それぞれを2進数に換算します。
2→0010 7→0111 1→0001 0→0000
最後に、それぞれの換算結果を並べて表記します。
換算結果:10011100010000
電卓ソフトを利用して各進数を換算
上記のように各進数を手計算で求める以外に、電卓ソフトを利用して換算する方法もあります。大きい数値を扱う場合には、電卓ソフトの方が計算間違いが起こりにくいと思います。
Windowsの電卓の場合
→→→を選択してください。電卓ソフトが起動します。
電卓が起動したら、メニューの→を選択してください。電卓が「プログラマ」モードに変化します。
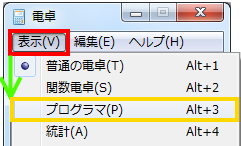
初めに、換算元の進数を選択します。ここでは[10進数]を選択しました。
次に数値を入力します。ここでは[200]を入力しました。
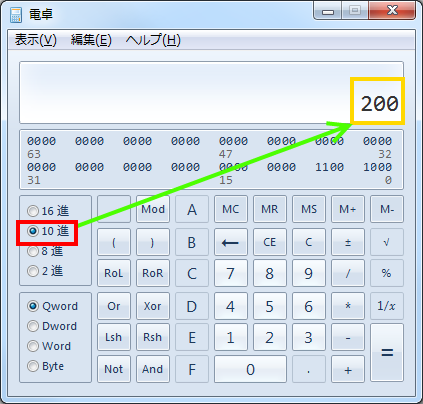
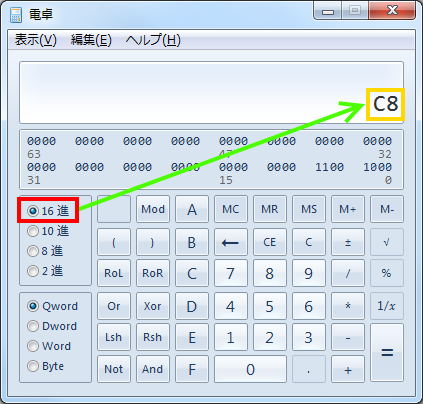
換算先の進数のラジオボタンをクリックします。ここでは[16進数]を選択しました。
クリックすると目的の進数で表示されます(16進数[C8]が表示)
元の表示に戻したい場合は、メニューの→を選択しましょう。
ビットとバイトとオクテット
コンピュータ内部のデータ処理の基本単位は、2進数の1桁分となります。これをbit(ビット:binary digitの略。2進数の1桁の意)と呼びます。
bitをコンピュータ上の情報処理の単位として使用する事を考えたのは、上に触れたシャノンです。
1bitでは、0と1という2通りの情報しか表現できません(二元符号)。
そのため、多くの種類の情報を扱いたい場合、大きい数値を扱いたい場合には、複数のbitをまとめて別な一つの単位として取り扱うようにしました。この単位を「byte(バイト)」とか「octet(オクテット)」とか呼びます。
- 1桁=0と1の二通り
- 2桁=00 01 10 11の四通り
- 3桁=2の3乗=八通り
- (中略)
- 8桁=2^8=256通り
(中略)
- 16桁=2^16=65536通り
1byte=8bitがよく使われますが、実は1byteが何bitを表すかは、利用するコンピュータシステムによって異なります。1byte=7bitという場合もありますので覚えておいてください。これは、元々byteという単位が、欧文文字コード一文字分という枠組みで設定された事に起因するそうです。
従って、8bitを基本的なまとまりとして把握したい場合には、必ず8bit=1octetとなるオクテット(octet)が表記法として選択される場合があります。
1バイト(オクテット)には、2の8乗=256通りのデータが格納できます
- 0→1ビット(1桁)
- 00000000→1バイト(オクテット)(8桁)
バイトやオクテットを情報の単位として使用する場合、0や1といった最小の情報量(1bitで表現可能な場合)でも利用した桁数全てを使用する必要があります。
- 1桁しか使わない場合の1=1=1bitのデータ量が必要
- 8桁利用した場合の1=00000001=8bitのデータ量が必要
補足:データ量の単位(接頭辞)
上記の通り、コンピュータのデータは二進法で処理されています。但し、情報量が多くなると数値の可読性が落ちますので、適宜大きい数値に関しては接頭辞をつけてより見やすい形で表記します。
ここで注意する必要があるのが、接頭辞を付す区切りとして十進法と二進法との二通り使用される点です。
繰り上がりの区切りとしては、10の累乗を対象とするSI(国際単位系)接頭辞が標準となっています。
しかし、コンピュータ上での情報処理については、2の累乗を区切りとした方が計算上便利なので、そちらも慣用的に使用されます。
| 単位(記号) | SI基準(十進区切り) | 慣用(二進区切り) |
|---|---|---|
| KB(キロバイト) | 103:千 | 210 |
| MB(メガバイト) | 106:百万 | 220 |
| GB(ギガバイト) | 109:十億 | 230 |
| TB(テラバイト) | 1012:一兆 | 240 |
| PB(ペタバイト) | 1015:千兆 | 250 |
| EB(エクサバイト) | 1018:百京 | 260 |
| ZB(ゼタバイト) | 1021:十垓 | 270 |
| YB(ヨタバイト) | 1024:一秭 | 280 |
先の1byteが何bitで構成されているか(8bit or 7bit)と同様に、この両者も共に使われています。
例えば、ハードディスクの容量を例にしてみましょう
- 250GBのハードディスク
- SI標準で計算:250×109=250,000,000,000
- 二進区切りで計算:250×230=268,435,456,000
単純に引き算すると、18,435,456,000(十進法で計算すると18.4GB、DVD-R4枚弱)もの容量の差が出てしまいます。もちろん、これは単なる数字上のマジックでしかないので、比較する事自体に意味はありません。
但し、パッケージなどのカタログ上では十進法表記されていても、Windowsのプロパティ表示では二進数表記が使われていたりしますので、同じメディアを使っていても容量表示が異なる場合も出てくるかもしれませんので、覚えておくとよいでしょう。
このような混同を防ぐために、特に二進法表記だと明示したい場合には、IEC(国際電気標準会議)が定めた二進接頭辞を用いて表記する事があります(一般生活上、こちらは余り見かけませんが)。
| IEC二進接頭辞(読み) | 値 |
|---|---|
| KiB(キビバイト) | 210 |
| MiB(メビバイト) | 220 |
| GiB(ギビバイト) | 230 |
| TiB(テビバイト) | 240 |
| PiB(ペビバイト) | 250 |
| EiB(エクスビバイト) | 260 |
| ZiB(ゼビバイト) | 270 |
| YiB(ヨビバイト) | 280 |
電卓ソフトを利用してデータ量を換算
データ量の単位の違いも、電卓ソフトを利用して換算をしましょう。この方が計算間違いが起こりにくいかと思います。
Windowsの電卓の場合
一例として[80GB(1000単位での換算)]の容量を持つハードディスクが、1024単位の換算でいくつになるか計算してみましょう。
→→→を選択します。電卓ソフトが起動します。
メニューの→を選択しましょう。電卓が[関数電卓モード]に変化します。
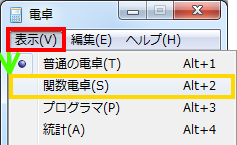
初めに、数値を入力します。ここでは[80]を入力しました。
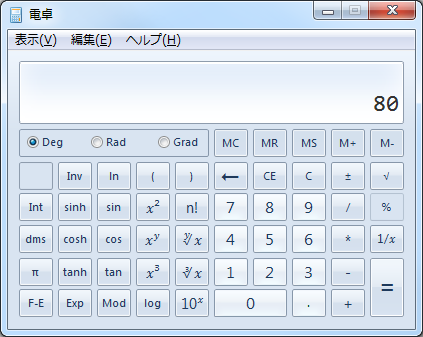
乗算(かけ算)のボタン*を左クリックします。
続いて、1000単位でのbyte量を求める計算を行いましょう。
[1000]を入力します。
[3乗の計算]をするボタンx3を左クリックします。
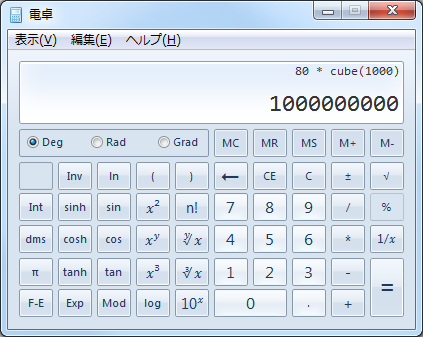
計算結果(イコール)のボタンを=左クリックします。
計算結果[80,000,000,000byte]が表示されます。
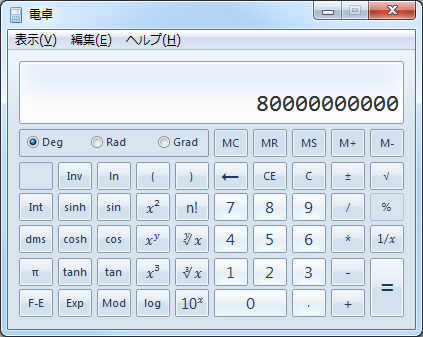
この計算結果を、1024単位で処理してみましょう。
除算(割り算)のボタン/を左クリックします。
[1024]を入力します。
[3乗の計算]をするボタンx3を左クリックします。
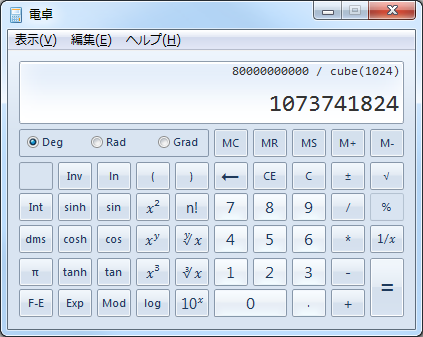
計算結果(イコール)のボタン=を左クリックします。
計算結果[74.5…(二桁以下略)byte]が表示されました。
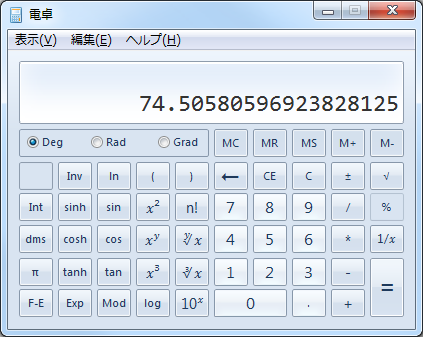
1024単位の場合、約74.5GBとなりました(実際には、メディアのフォーマット時のクラスタ指定やファイル保存の構造等の関係で保存可能な容量が決定しますので、容量いっぱいにデータが格納できるわけではありません)。
元の表示に戻したい場合は、メニューの→を選択しましょう。

Googleで換算しよう
ロボット型サーチエンジンの代表格として知られるGoogleですが、サーチエンジンとして使う以外にもさまざまな使用方法があります。ここではGoogleを電卓として使ってみましょう。
試しに、ここをクリックしてください。Googleで計算ができているでしょうか?
四則演算以外にも複雑な計算ができます。また、2進数、10進数、16進数の相互換算も可能です。電卓が利用できない場合にGoogleでちょっと計算という使い方も便利ですよ。
2進数の10011100010000を10進数、16進数にそれぞれ変換してみましょう。
- 10進数への換算
- 16進数への換算